Sonická tryska - průtok plynu
trocha teorie a praktický výpočet
Pro výpočty spojené s konstrukcí rebreatheru, avšak koneckonců i pro stanovení průtočného množství dýchacího plynu v systému s otevřeným okruhem, je častokrát třeba stanovit množství plynu proteklého za jednotku času tryskou dávkovacího zařízení. Tímto zařízením je obvykle redukční ventil, snižující vysoký tlak ze zásobníku plynu na středotlak a přivádějící plyn ke zmíněné trysce. Tlak za tryskou je pak v případě rebreatheru obvykle okolní tlak.
V těchto řádcích je za jednotku tlaku vzat 1 bar, jelikož ji používá většina technických potápěčů.
Plyn proudí z místa o větším tlaku p0 do místa o tlaku nižším p1 a tím současně dochází k jeho expanzi a změně teploty. Tento, tzv. adiabatický děj probíhá rychle, neuvažuje se výměna tepla s okolím. Pro ideální plyn je popisován rovnicí adiabaty:
Teplota se dopočítá pomocí běžné stavové rovnice ideálního plynu (zde pro jednotkové množství):
Poissonova konstanta je podílem specifických tepel plynů c při stálém tlaku a při stálém objemu:
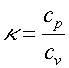
Hodnota Poissonovy konstanty je pro každý plyn specifická a v termodynamice bývá odvozováno, že přibližně platí:
| | pro plyny s molekulou |
| 1,67 | jednoatomovou (např. He, Ar) |
| 1,40 | dvouatomovou (např. O2, N2 a jejich směsi - vzduch, nitrox) |
| 1,33 | tří- a víceatomovou (např. CO2) |
Experimentálně stanovené údaje pro plyny, které nás mohou zajímat, jsou uvedeny v tabulce spolu s jejich hustotami (měrnými hmotnostmi) ![]() za normálních podmínek (teplota 0°C, tlak 1 bar) a jejich molárními hmotnostmi
za normálních podmínek (teplota 0°C, tlak 1 bar) a jejich molárními hmotnostmi ![]() .
.
| Plyn | (kg/m3) |
(kg/kmol) |
|
| vzduch | 1,406 | 1,276 | 28,96 |
| N2 | 1,404 | 1,234 | 28,01 |
| O2 | 1,416* | 1,409 | 32,00 |
| He | 1,630 | 0,176 | 4,00 |
| Ar | 1,668 | 1,759 | 39,95 |
| Ne | 1,64 | 2,277 | 50,49 |
| CO2 | 1,304 | 1,951 | 44,01 |
| H2 | 1,41 | 0,0089 | 2,02 |
| * publikované hodnoty se pohybují v mezích 1,40 - 1,416 | |||
Pro směsi plynů můžeme orientačně - v přiblížení ideálního plynu - získat hodnoty uvedených veličin prostřednictvím váženého průměru. Například hodnotu pro EAN 32 získáme výpočtem
Rovnici adiabaty pro změnu stavu plynu lze rovněž napsat v jiném tvaru:
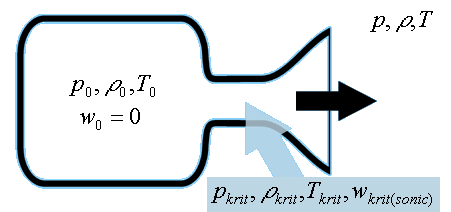
Rychlost výtoku plynu
Při výtoku tekutiny (tedy i plynu) z nádoby musí platit zákon zachování energie, který bývá vyjádřen Bernoulliho rovnicí, říkající, že v každém okamžiku musí být součet kinetické a potenciální energie konstantní. Potenciální energie je dána součtem tlakové a gravitační energie a platí:
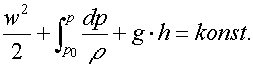
V tomto vztahu w označuje rychlost, a g.h je gravitační potenciální energie, která převažuje v případě kapaliny, avšak je zcela zanedbatelná pro plyn, jehož potencíální energie je skryta především v jeho stlačeném objemu -zde představovanou integrálem. Předpokládejme, že plyn vytéká tryskou z místa, v němž je v klidu (není to zcela pravda, jelikož výpočty se budou provádět pro proudění ze středotlaku do tlaku okolí a navíc středotlaký plyn je obvykle poněkud ochlazen původní expanzí z vysokého tlaku. Chyba, které se dopouštíme, je však zanedbatelná.). Pak můžeme konstantní hodnotu na pravé straně rovnice položit rovnu nule a dostáváme:
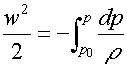
Dosazením vyjádření pro hustotu z rovnice adiabaty a vyřešením uvedeného integrálu
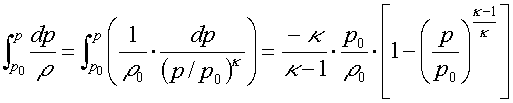
dostaneme pro rychlost plynu
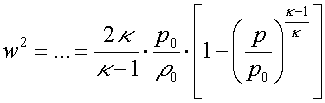
Rychlost výtoku plynu v nejužším ("kritickém") místě nemůže být větší než lokální rychlost zvuku (lokální, jelikož je závislá na teplotě). Přitom pro rychlost zvuku platí vztah
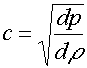
ze kterého opět dosazením hustoty z rovnice adiabaty obdržíme přes
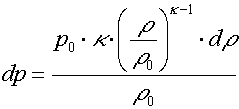
a dosazením za dp
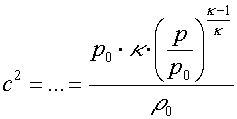
Má-li tedy být rychlost výtoku rovna rychlosti zvuku, tedy položíme-li c2=w2, vyplyne nám po dosazení z předchozích vztahů pro poměr p/p0, tedy pro poměr výstupního tlaku ke vstupnímu, podmínka:
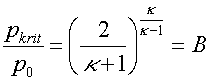
Zde pkrit je kritický tlak dosažený v kritickém (nejmenším) průřezu trysky a tento vztah říká, že je-li výstupní tlak p menší nebo rovenpkrit , tj. platí-li p/p0=<B, je v kritickém průřezu dosaženo lokální rychlosti zvuku wkrit, která nemůže být překročena při žádném dalším zvyšování vstupního tlaku p0. O lokální rychlosti zvuku přitom hovoříme proto, že rychlost zvuku je závislá na teplotě plynu a ta je v kritickém průřezu jiná než na vstupu, jak uvidíme dále. Rychlost proudění v trysce získáme dosazením tohoto poměru do předchozího vztahu jako
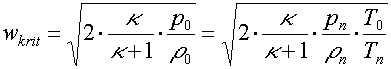
jelikož ze stavové rovnice je
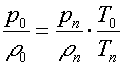
Převrácená hodnota poměru, tj. poměr
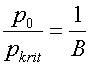
má pro jednotlivé dýchací plyny připadající v úvahu hodnoty mezi 1,90 až 2,05, tedy v průměru přibližně 2. Znamená to, že pokud tlak (p0) před tryskou bude alespoň dvojnásobkem tlaku (p) za ní, bude rychlost v nejužším místě rovna rychlosti zvuku (sonické či také kritické proudění). Bude-li však tento poměr menší, např. 1,5, bude plyn tryskou proudit rychlostí nižší.
Z toho plyne následující: máme-li např. tlak před tryskou p0 stálý a roven 10 bar (1000 kPa), bude při potápění výtok z ní do okolního tlaku sonický do hloubky, v níž bude okolní tlak poloviční, tj. do hloubky 40 metrů (v níž je p=5 bar). Rychlost proudění v trysce bude pro vzduch, který měl před tryskou teplotu rovnou 0 °C v každé hloubce rovna 303 m/s. Půjdeme-li však hlouběji, rychlost výtoku se bude snižovat (proudění bude subsonické) a např. v hloubce 60 m pro vzduch obdržíme
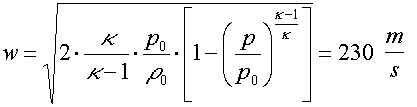
v hloubce 80 m jen 105 m/s, přičemž v hloubce 90 m (kde tlak ph=10 bar) by proudění zcela ustalo.
Pro hustotu a teplotu plynu v trysce při sonickém proudění lze odvodit vztahy
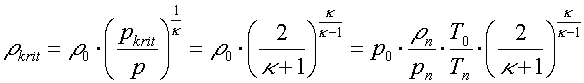
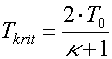
Všimněme si, že i zde jsou kritická hustota i teplota závislé na druhu plynu a na jeho vstupní teplotě i hustotě a rovněž na vstupním tlaku. Pro výše uvedený příklad vychází kritická hustota na 6,73 kg/m3 a kritická teplota na 227 K (-46 °C).
Vytékající množství
Hmotnostní množství plynu proteklého tryskou za jednotku času dM/dt lze stanovit ze vztahu
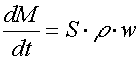
Proteklé množství plynu se však častěji uvádí v "normálních" objemových jednotkách za jednotku času (např. v litrech za minutu). Normálním objemem rozumíme objem vztažený k normálním podmínkám (na hladině). Tuto veličinu Dn jsme schopni stanovit jednoduše tak, že hmotnostní množství vydělíme normální hustotou plynu, tedy
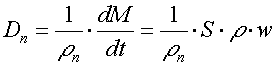
Pro sonický průtok zde využijeme kritických hodnot a obdržíme
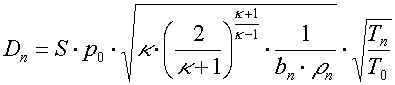
V tomto vztahu je několik konstant charakteristických pro daný plyn a ty lze zahrnout do jedné konstanty s výsledkem
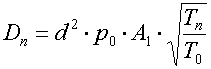
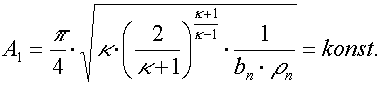
Zahrneme-li do konstanty i vztahy pro přepočet jednotek (tlak v barech, průměr trysky v milimetrech a průtok v litrech za minutu, obdržíme místo A1 konstantu A, která umožňuje jednodušší výpočty průtoku pro běžně používané dýchací směsi. Jednoduchou analýzou lze obdržet pro konstantu A následující zjednodušené vztahy:
A = 8,65 pro čistý kyslík
A = 9,233 - 0,00588×O2 pro nitrox (koncentrace O2 v %)
A = 9,71 + 0,0011×He2 pro trimix (He v mezích 10 - 50 %, koncentrace He v %)
- Příklad
- TMX 20/50, d = 0,31 mm, p0 = 11 bar, t =0 °C
A = 9.71 + 0.0011 × 502 = 12.46
Dn = A × p0 × d2 = 12.46 × 11 × 0.312 = 13,17 l/min
(přesnější výpočet podle původní (složitější) rovnice dává 12,91 l/min)
Použití výpočtů pro rebreathery
Ve výše uvedených výpočtech byly jako p0 a pamb uvedeny středotlak a tlak okolí (v barech). Středotlak p0 je konstantní, je-li redukční ventil (první stupeň) uzavřený (nekompenzovaný na tlak okolí). V opačném případě, při použití prvního stupně plicní automatiky, kdy je redukční ventil otevřený (kompenzovaný na tlak okolí), středotlak [bar] stoupá s přírůstkem hloubky h [m] o h/10.
Nekompenzovaný redukční ventil
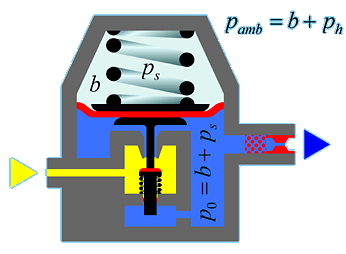
V tomto obrázku b představuje normální atmosférický, ps tlak vyvolaný silou řídicí pružiny (ve skutečnosti středotlak měřený běžným manometrem) a ph je hydrostatický tlak. pamb zastupuje ("absolutní") okolní tlak.
Nekompenzovaný redukční ventil bývá využíván tam, kde je nutno dosáhnout konstantního průtoku nezávislého na hloubce, t.j. k získání stálé dávky
- diluentu v rebreatheru s polouzavřeném okruhu se stálou dávkou (constant mass flow - CMF SCR, např. Dolphin)
- kyslíku v ručně řízeném rebreatheru s uzavřeným okruhem (manually controlled - MC CCR, např. KISS)
Maximální přípustná hloubka jeho použití je hloubka, do níž je zachován sonický průtok, t.j. hloubka, ve které je okolní tlak pamb přibližně roven polovině středotlaku p0. Ve větších hloubkách je průtok subsonický a proteklé množství tedy klesá s rostoucí hloubkou.
- Příklad 1
- je-li p0 = 12 bar, pak maximální hloubka, ve které je průtok ještě sonický, je okolo 50 metrů (pamb = 6 bar).
- Příklad 2
- je-li p0 = 11 bar a průměr trysky d = 0,08 mm, je průtok čistého kyslíku tryskou 0,61 l/min
v každé hloubce do 45 m, avšak v hloubce 90 m subsonický průtok zajistí pouze 0,36 l/min! K použití do
90 m je zapotřebí středotlaku p0 >= 20 bar. Pak ovšem k zajištění požadovaného průtoku
(např. 0,8 l/min) musí být průměr trysky menší, jelikož původní tryska by dávala průtok 1,1 l/min. V tomto
případě by měl být
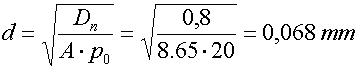
Kompenzovaný redukční ventil
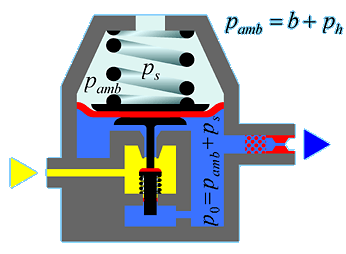
U otevřeného prvního stupně (používaného rovněž v běžných plicních automatikách) s rostoucí hloubkou roste i středotlak podle vztahu p0 = ps + b + h/10. Z předchozích úvah víme, že tím roste i dávka (Dn =A . p0 . d2). V tomto případě je dávka Dh v hloubce dána dávkou D0 na hladině násobenou poměrem středotlaků v hloubce a na hladině p0h/p00, tedy
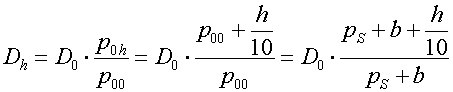
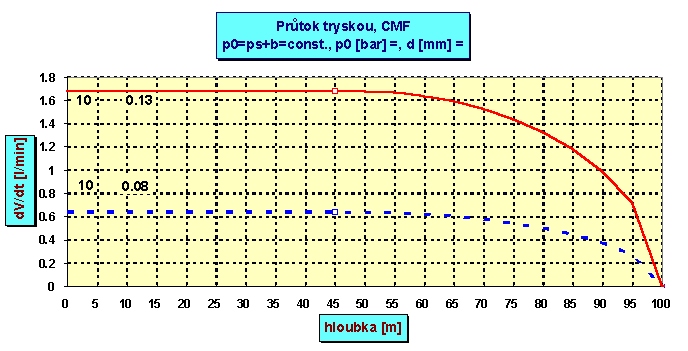
a s hloubkou lineárně narůstá. V určité hloubce hkrit dané konstantou B pak okolní tlak vůči vstupnímu tlaku p0 nabude kritické hodnoty pkrit a rychlost proudění se sníží na podzvukovou. Dávka sice s hloubkou stále narůstá, avšak už ne lineárně, jak je znázorně v následujícím grafu, ve kterém je pro dobrou demonstraci zvolen nižší středotlak. Dávka je stanovena pro průtok dvěma paralelními tryskami o průměrech 0,2 mm.
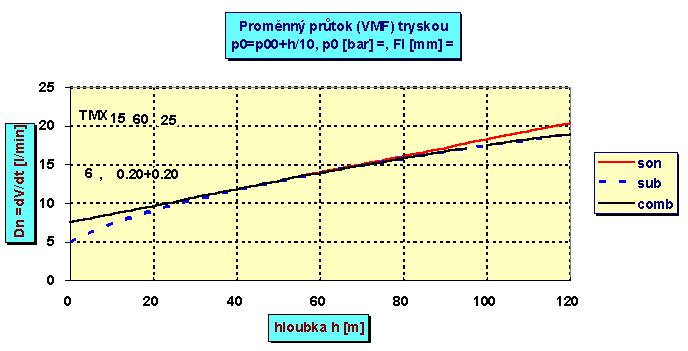
Způsobu dávkování s kompenzovaným redukčním ventilem využívají např. Ray nebo Azimuth.
Zmíněnou kritickou hloubku lze snadno nalézt úvahou, podle níž velikost středotlaku v hloubce p0h musí být přibližně rovna dvojnásobku tlaku okolí pamb, tj. ps + pamb = 2×pamb. To totiž znamená, že průtok začne být podzvukový v hloubce, ve které bude tlak okolí pamb roven tlaku vyvolanému silou pružiny ps (což je, jak již bylo řečeno, tlak, který měříme manometrem při nastavování středotlaku). Tzn. máme-li ps = 10 bar, průtok přestane být sonický v hloubce 90 m, v níž je tlak roven pamb = 10 bar. Avšak ještě v hloubce 200 m bude průtok jen o několik procent nižší, než průtok vypočítaný pomocí "sonické" rovnice, jelikož současně s hloubkou roste i středotlak a tím i hustota směsi.
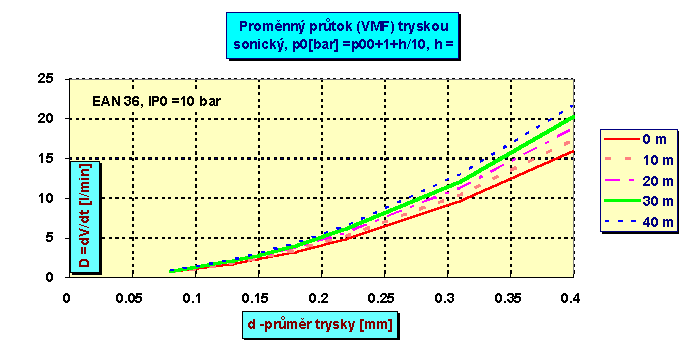
Na dalším obrázku je znázorně průtok směsi (EAN 36) tryskou v závislosti na jejím průměru a na hloubce.
Výhody a nevýhody obou uspořádání
Výhodou použití nekompenzovaného redukčního ventilu je zachování stálého průtoku ve vhodném rozmezí hloubek. Proto také dávka dodávané směsi D je skutečně neměnná s hloubkou a například podle základního vztahu pro výpočet složení směsi ve vaku polouzavřeného okruhu
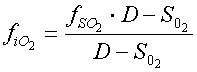
fSO2 je podíl kyslíku v dodávané směsi
SO2 je minutová spotřeba kyslíku
fiO2 je podíl kyslíku ve vaku
Podíl kyslíku ve vaku není závislý na hloubce. Proto při vhodné volbě středotlaku a trysky udržuje průtok tryskou parciální tlak kyslíku v bezpečných mezích. Ze známého podílu kyslíku lze rovněž snadno stanovit podíl inertních plynů ve směsi pro dekompresní účely.
Zvolíme-li např. p0 = 18 bar, je zajištěn konstantní průtok směsi do hloubky okolo 80 metrů. Je však nutné vhodně vybrat průměr trysky (malý), aby průtok nebyl zbytečně velký. Konstantní průtok umožňuje rovněž s velkou přesnosti stanovit potřebnou zásobu směsi.
Poznámka: výše uvedené platí pro přístroj s jedním vakem (nádechovým). Při použití odděleného výdechového vaku s přetlakovým ventilem je podíl kyslíku ve vaku fiO2 poněkud vyšší, parciální tlak kyslíku piO2 je asi o 5 kPa (0,05 bar) vyšší nezávisle na hloubce.
Ohledně uzavřeného okruhu s manuálním řízením dodávky kyslíku (rebreather KISS a jeho klony) je nutno podotknout, že pro potápěče je životně důležité, aby stálá dávka kyslíku zůstala pod základní metabolickou spotřebou, t.j. přibližně pod 0,8 až 1,0 litrů za minutu. Proto také průměr trysky musí být dostatečně malý (viz dříve uvedený příklad č. 2). Aby se předešlo ucpání tak malé trysky, bývá navíc trysce předřazen filtr 10 až 20 mikrometrů. (Místo kruhové trysky bývá používán i nastavitelný jehlový ventil - otázkou je jeho chování v prostředích o různých teplotách a jeho případné seřizování pod vodou).
Použití kompenzovaného redukčního ventilu zvyšuje s hloubkou dávku směsi. Nevýhodou tohoto uspořádání je pouze méně snadné stanovení potřebné zásoby směsi. Na druhé straně zvýšený průtok "vylepšuje" podíl kyslíku fiO2 v dýchané směsi, tj. jeho podíl ve směsi se s hloubkou rychleji a více blíží k jeho podílu v zásobníku (a i kdyby byl stejný, musel být stanoven tak, aby jeho parciální tlak nepřekročil předepsanou mez ani v největší hloubce). Takže podíl kyslíku ve směsi lze rovněž stanovit pomocí výše uvedeného vztahu a dávky D0 stanovené na hladině, pouze hodnota fiO2 bude poněkud podceněna. Navíc průtok je sonický v podstatně větších hloubkách a i subsonický zajišťuje dostatečnou dávku směsi. To umožňuje dosáhnout větších hloubek i při menším základním středotlaku (ps). Výhodou je rovněž to, že z kompenzovaného prvního stupně lze vyvést hadici ke druhému stupni plicní automatiky k použití pro nouzový přechod na otevřený okruh (bailout).
Ke stanovení zásoby směsi pro zamýšlený ponor je vhodné použít vztahu pro dávku v největší hloubce
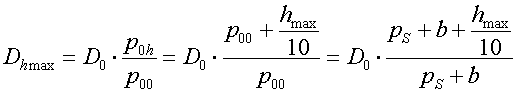
kde ps je středotlak stanovený manometrem na hladině (tedy přetlak vůči atmosférickému tlaku b) a D0 je hladinová dávka stanovená např. průtokoměrem.
Praktická realizace trysky
Uvedené výpočty průtoků byly odvozeny za předpokladu, že jde o ideální plyn protékající zcela hladkou a krátkou kruhovou tryskou. Její tvar a kvalita povrchu její stěny mohou pochopitelně velikost průtoku ovlivnit. Proto je nutno uvedené výpočty chápat jako orientační pro odhad velikosti trysky nebo průtoku a v praktickém použití vždy průtočné množství stanovit experimentálně.
Jelikož trysky mívají malý průřez a mohly by se ucpat, bývají častokrát zdvojeny a opatřeny předřazeným filtrem.
